Не хватало терпения и времени сделать это для случая курносого куба. В конце концов, вожделенные координаты обнаружились в Википедии: http://en.wikipedia.org/wiki/Snub_cube
Координаты вершин этого многогранника находятся как множество перестановок наборов троек:
(±1, ±ξ, ±1/ξ)
причем, с четным числом положительных чисел в тройке надо брать все четные, а с нечетным числом положительных - все нечетные перестановки. Запутанно, но разобраться можно. Число ξ является действительным корнем уравнения:
ξ**3+ξ**2+ξ=1,

Значение можно получить по формуле:

Оказалось, что курносый куб в каком-то смысле настоящий уродец. Внешне сам многогранник выглядит довольно оригинально. Квадратные грани, окруженные треугольниками, повернуты относительно друг друга под углом. В этом, видимо и состоит курносость этой модели. Возможно, курносым его называют еще и потому, что эту форму можно вписать в куб так, что квадратные грани будут лежать на соответствующих сторонах куба. Форма весьма привлекательная.

"Уродство" модели проявляется в его несимметричности, в ней представлены только симметрии вращения. Многогранник не обладает зеркальной симметрией. Существуют две разновидности этого многогранника, которые можно получить зеркальным отражением. Можно говорить о правом и левом курносом кубе.

Только вот какой левый, а какой правый?

На этом видимые недостатки исчерпываются. Заглянем во внутреннюю кухню мира этого многогранника и его звездчатых форм.

У курносого куба три вида граней:

1. квадратные (на изображении зелёного цвета) - шесть штук
2. треугольные, примыкающие к квадратам (желтые) - 24 штуки
3. треугольные, вершины которых совпадают с вершинами трех квадратов (синие) - восемь штук

Соответственно имеем три эпюры, соответствующие этим типам граней:

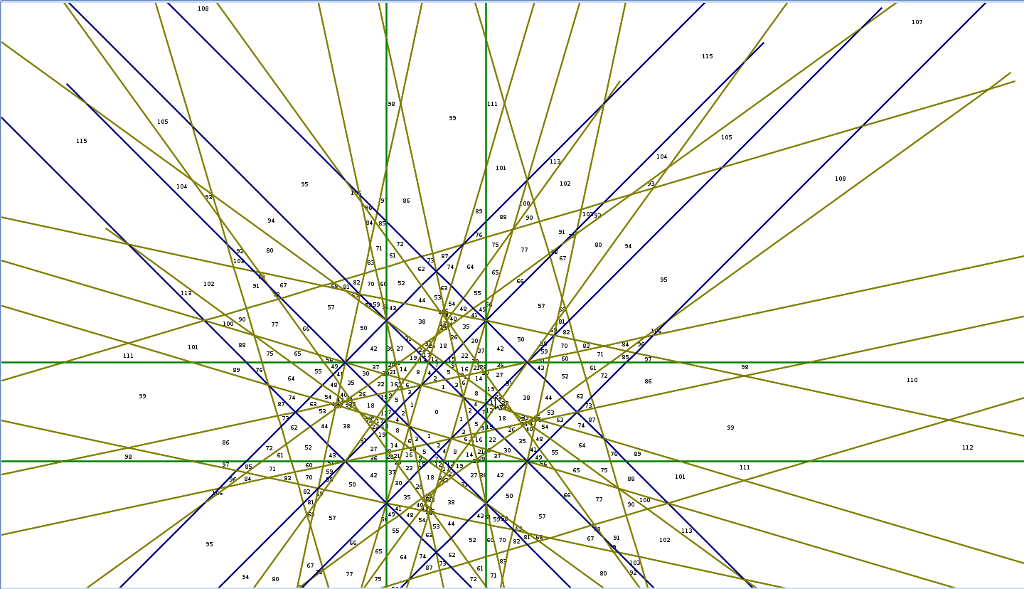
Эпюра квадратных граней

Эпюра треугольных примыкающих граней

Эпюра курносых треугольников

Собственно, вся несимметричность сосредоточенна на второй эпюре. Первая и третья эпюры вполне себе симметричны. Вторая эпюра совершенно несимметрична. Эта особенность приводит к интересному поведению звездчатых форм. Оказалось, что комбинировать грани так, чтобы получилось что-то внятное довольно сложно, по сравнению с полностью симметричными моделями. Собственно, первая звездчатая форма получается достаточно легко. Это все многоугольники, примыкающие к базовым (номер 0 на эпюрах) на всех трех эпюрах. Получаем вот такой "шарик":

Вторую звездчатую форму тоже получить легко. Достаточно взять следующий ободок многоугольников на каждой из эпюр. Получаем модель:

Дальше оказалось, что действовать по стандартной схеме наращивания слоя за слоем многоугольников на эпюрах не получается. В чем дело? На изображении второй формы видно некоторое "засилье" желтых граней. Это грани несимметричной части модели. Вот они-то и мешают нормальному для остальных многогранников процессу построения звездчатых форм. Их очень много и они все нарушают симметрию. Можно сказать, что вся не симметрия сосредоточена на второй эпюре.

После некоторых мук удалось научиться комбинировать многоугольники на эпюрах так, чтобы получались замкнутые тела. Идея состояла в том, что мы начинаем с граней первой или третьей эпюры. Оставшиеся отверстия в многограннике пытаемся заполнить гранями, соответствующими второй, несимметричной, эпюре.
Легко создавать многогранники, содержащие только две эпюры, например многогранник "Сюрикен 3D" получается из многоугольников только из второй и третьей эпюры:

Так же легко получить многогранники, состоящие из граней, соответствующие только одной второй эпюре, вот парочка тахих:

Многогранник "Шинокол"

Многогранник "Шинорез"

Несмотря на не симметричность второй эпюры звездчатые формы из нее получаются вполне симметричными.

Напоследок еще несколько форм курносого куба, которые удалось получить после некоторых мытарств.

Первая представляет собой куб с надрезанными ребрами на гранях которого располагаются повернутые друг относительно друга четырехугольные пирамиды:

Куб с гравировкой

Вторая модель - это октаэдр из граней которого как бы выступает другой звездчатый многогранник:

Октаэдральная форма

И, наконец, псевдо-симметричная форма курносого куба:

Псевдо-симметричная форма

Все модели, представленные в статье можно рассмотреть в интерактивном режиме с разных сторон. Каждая картинка ведет на страничку с интерактивной моделью. Визуализатор моделей реализован в технологии WebGL, поэтому для просмотра Вам потребуется современный браузер, поддерживающий технологию WebGL. Например, Chrome или Firefox4.

В таблице ниже представлена классификация представленных многогранников в соответствии с нумерацией эпюр:

Название	Классификация	Изображение
Курносый куб	{(0)(0)(0)}
1-ая звездчатая форма	{(1)(1,2,3)(1)}
2-ая звездчатая форма	{(2,3)(4,5,6,7,8,9)(2,3)}
Сюрикен 3D	{(4,5,6,7)(10,11,12,13,14,15,16,17,18,19,20,21) (2,3,4,5,7,8,9,10,14,15,16,21,22)}
Шинокол	{()(11,12,24,26,40,41,44,45,62,63,64,68,85,86,87, 88,89,90,93,94,95,96,113,115, 116,117,121,122,142, 143,144,149,173,174,182,209,211,252,253,295)()}
Шинорез	{()(72,99,100,126,127,130,134,152,153,156,157,158, 159,162,185,186,187,188,189,191,192,193,194,195, 196,197,200,226,227,228,229,230,231,232,233,234, 236,237,239,265,266,267,268,269,271,272,274,277, 278,279,309,312,316,323)()}
Куб с гравировкой	{(1,2,3,4,5,6,8,9,10,11,14,16,20,21,28)(0,1)(0,1,3,6)}
Октаэдральная форма	{(4,5,6,7)(10,11,12,13,14,15,16,17,18,19,20,21) (2,3,4,5,7,8,9,10,14,15,16,21,22)}
Псевдо-симметричная форма	{(2,3,6,11)(6,7,14,15,17,29,32,53)(2,3,4,9,15)}

Все модели созданы в редакторе многогранников PolyhedronEditor